代码随想录_栈与队列

栈与队列

232.用栈实现队列

232. 用栈实现队列

使用栈实现队列的下列操作：

push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。

思路: 定义两个栈: 入队栈, 出队栈, 控制出入栈顺序, 进入的元素倒两次就是原顺序

代码:

java">class MyQueue {
    Stack<Integer> in;
    Stack<Integer> out;

    public MyQueue() {
        in = new Stack<>();
        out = new Stack<>();
    }
    
    public void push(int x) {
        in.push(x);
    }
    
    public int pop() {
        inToOut();
        return out.pop();
    }
    
    public int peek() {
        inToOut();
        return out.peek();
    }

    private void inToOut() {
        // out非空时不能往里面倒, 出的时候要先把out里的出完, 再倒入
        // 否则原来的数据会被覆盖
        if(!out.isEmpty()) return;

        while(!in.isEmpty()) {
            out.push(in.pop());
        }
    }
    
    public boolean empty() {
        return in.isEmpty() && out.isEmpty();
    }
}

225. 用队列实现栈

使用队列实现栈的下列操作：

push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空

思路: 每次pop, peek都要reposition

代码:

java">class MyStack {
    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }
    
    public void push(int x) {
        queue.offer(x);
    }
    
    public int pop() {
        reposition();// 每次pop时将队列前size - 1个放到队列末尾
        return queue.poll();
    }
    
    public int top() {
        reposition();// 每次pop时将队列前size - 1个放到队列末尾
        int n = queue.poll();
        queue.offer(n);
        return n;
    }
    
    public boolean empty() {
        return queue.isEmpty();
    }

    private void reposition() {
        int size = queue.size();
        size--;
        while(size-- > 0) {
            queue.offer(queue.poll());
        }
    }
}

20. 有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

思路:

一共有三种情况:

字符串里左方向的括号多余了，所以不匹配。
括号没有多余，但是括号的类型没有匹配上。
字符串里右方向的括号多余了，所以不匹配。

每一个左括号, 压入对应的右括号, 当开始遍历右括号时, 按照如下方式和栈中元素进行对比

代码:

java">class Solution {
    public boolean isValid(String s) {
        // 0. 剪枝
        int len = s.length();
        if(len % 2 != 0) return false;// 长度为奇数, 则一定不能匹配

        // 1. 初始化栈
        Stack<Character> stack = new Stack<>();

        // 2. 遍历每一个字符
        for(int i = 0;i < len;i++) {
            // 2.1 每一个左括号, 压入对应的右括号
            if(s.charAt(i) == '(') {
                stack.push(')');
            }else if(s.charAt(i) == '[') {
                stack.push(']');
            }else if(s.charAt(i) == '{') {
                stack.push('}');
                // 2.2 每一个右括号, 查看栈中对应的右括号是否相等
            }else if(stack.isEmpty() || s.charAt(i) != stack.peek()) {
                // 不能是s.pop,否则在判断时就会将元素弹出
                return false;
            }else {// 右括号匹配, 出栈
                stack.pop();
            }
        }

        // 3. 遍历完后, 查看栈中是否还有右括号(左括号多余)
        return stack.isEmpty();
    }
}

1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入：“abbaca”
输出：“ca”
解释：例如，在 “abbaca” 中，我们可以删除 “bb” 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”，其中又只有 “aa” 可以执行重复项删除操作，所以最后的字符串为 “ca”。

法一: 栈

思路: 用字符串模拟栈(也可以直接用栈, 需要再转为字符串)进行"消消乐", 留下的就是最终的字符串

代码:

java">class Solution {
    public String removeDuplicates(String s) {
        // 1. 定义字符串模拟栈
        StringBuilder sb = new StringBuilder();
        // 2. 遍历s的每一位, 与栈进行消除
        int top = -1;
        for(int i = 0;i < s.length();i++) {
            if(top >= 0 && s.charAt(i) == sb.charAt(top)) {
                sb.deleteCharAt(top--);
            }else {
                sb.append(s.charAt(i));
                top++;
            }
        }
        // 3. 返回
        return sb.toString();
    }
}

法二:双指针

思路: 快指针指向原字符串要处理的字符, 慢指针指向新的字符串, 当新字符串出现相邻相等的情况, 则将两个同时排除, 回退到第一次出现该字符的位置, 继续遍历原字符串的下一个字符, 否则, 快慢指针同时往前走.

代码:

java">class Solution {
    public String removeDuplicates(String s) {
        // 1. 初始化
        char[] str = s.toCharArray();
        int fast = 0,slow = 0;
        
        // 2. 遍历原字符串
        while(fast < str.length) {
            str[slow] = str[fast++];
            // 2.1 新的字符串出现成对可消除, 走到第一次出现的位置, 覆盖(同时消除)
            if(slow > 0 && str[slow] == str[slow - 1]) {
                slow--;
            }else{
                // 2.2 没有可消除的字符, fast slow都往后走
                slow++;
            }
        }
        
        // 3. 返回
        return new String(str,0,slow);
    }
}

150. 逆波兰表达式求值

根据逆波兰表示法，求表达式的值。

有效的运算符包括 + , - , * , / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：

整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入: [“2”, “1”, “+”, “3”, " * "]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

思路: 栈, 每遇到一个操作符, 就对栈中的两个数组进行计算, 注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序.

代码:

java">class Solution {
    public int evalRPN(String[] tokens) {
        // 0. 剪枝
        if(tokens.length == 1) return Integer.valueOf(tokens[0]);

        // 1. 定义栈
        Stack<Integer> sk = new Stack<>();
        // 2. 逐个处理
        for(String s : tokens) {
            // 2.1 处理运算符
            if("+".equals(s) || "-".equals(s) || "*".equals(s) || "/".equals(s)) {
                // 注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序
                int n = sk.pop();
                int m = sk.pop();
                if("+".equals(s)) {
                    sk.push(m + n);
                }else if("-".equals(s)) {
                    sk.push(m - n);
                }else if("*".equals(s)) {
                    sk.push(m * n);
                }else if("/".equals(s)) {
                    sk.push(m / n);
                }
            }else {
                // 2.2 处理数字
                sk.push(Integer.valueOf(s));
            }
        }
        // 3. 返回
        return sk.pop();
    }
}

239. 滑动窗口最大值

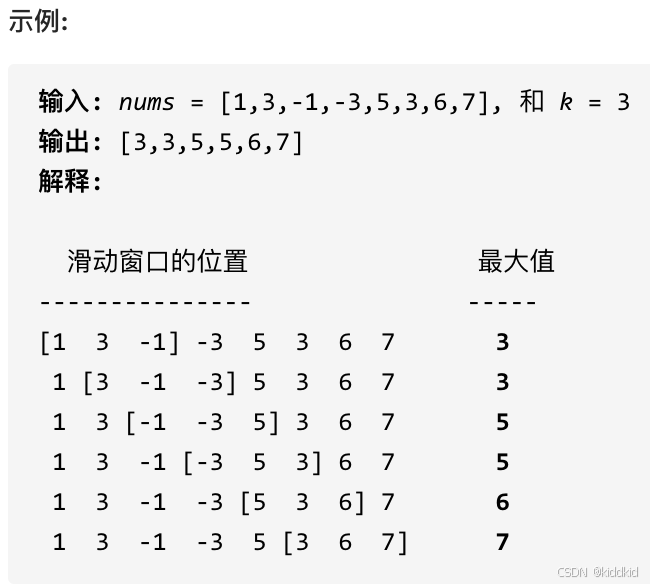
给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

提示：

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length

思路: 单调队列, 保证队头为窗口内最大值, 保证每次队列内有不多于k个元素

代码:

java">class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 1. 定义容器
        ArrayDeque<Integer> q = new ArrayDeque<>();
        int n = nums.length,index = 0;
        int[] ans = new int[n - k + 1];

        // 2. 循环遍历
        for(int i = 0;i < n;i++) {
            // 2.1 出: 将不符合窗口范围的移出
            while(!q.isEmpty() && q.peek() < (i - k + 1)) q.poll();

            // 2.2 入: 先将比该数值小的从后往前依次移出(保证单调), 再放入
            while(!q.isEmpty() && nums[q.peekLast()] < nums[i]) q.pollLast();
            q.offer(i);

            // 2.3 收集: 当窗口中走够k个元素时, 开始收集
            if(i >= k - 1) ans[index++] = nums[q.peek()];
        }

        // 3. 返回
        return ans;
    }
}

347.前 K 个高频元素

347. 前 K 个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

思路: map统计num及其出现次数, PriorityQueue用作小顶堆, 维护前k个出现次数最多的entry

代码:

java">class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 1. 定义容器
        int[] ans = new int[k];
        Map<Integer,Integer> map = new HashMap<>();
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1,o2) -> o1[1] - o2[1]);

        // 2. 填充map
        for(int num : nums) {
            map.put(num,map.getOrDefault(num,0) + 1);
        }

        // 3. 填充pq
        Set<Map.Entry<Integer,Integer>> entries = map.entrySet();
        for(Map.Entry<Integer,Integer> e : entries) {
            int[] t = new int[2];
            t[0] = e.getKey();
            t[1] = e.getValue();
            pq.offer(t);
            // 维持小顶堆中3个出现次数最多元素
            if(pq.size() > k) pq.poll();
        }

        // 4. 返回
        for(int i = 0;i < k;i++) {
            ans[i] = pq.poll()[0];
        }

        return ans;
    }
}